목차
이 포스팅은 weights initialization 기법들의 수식, 특징, 사용처를 설명합니다. keras에서 기본적으로 제공하는 기법들을 위주로 정리하였습니다.
· 들어가며
· 웨이트 초기화 기법 분류
- 상수 기반 초기화
- 선형 대수 기반 초기화
- 확률 분포 기반 초기화
- 분산 조정 기반 초기화
· fan in, fan out
· Lecun Initialization
· Xavier Glorot Initialization
· He Initialization
· 마치며
들어가며

이번 포스팅에서는 weight 값을 어떻게 초기화 시킬 수 있는지에 대해서 알아보겠습니다. 웨이트 값을 어떻게 초기화 시키는 지에 따라서 그라디언트를 얼마나 잘 전달할 수 있고, 레이어를 더 많이 쌓을 수 있는지를 좌우한다고 합니다. 위 도표는 웨이트 초기화 방법에 따라서 어떻게 Z-value, Activations, Gradients 등이 달라지는 지를 시각적으로 표현해준 것입니다. 이와 관련된 더 자세한 이론적 배경은 다음 자료를 참고해주시면 감사하겠습니다.[1]
텐서 플로우에선는 웨이트를 초기화 할 때에는 GlolotUniform 기법을 사용합니다. ResNet과 같은 모델 구현체를 보면 he_normal 기법을 사용하기도 합니다. 이번 포스팅에서는 이러한 초기화 방법들의 개념들을 쉽게 정리해보도록 하겠습니다. 이론적 배경이 궁금하신 분들은 [1]이나 [2] 포스팅을 참고해주세요.
그럼 시작하겠습니다.
웨이트 초기화 기법 분류
웨이트 초기화 기법들을 정리하면서 크게 세 가지 범주로 구분하여 보았습니다. 학계에서 이렇게 딱 나눠놓은 것은 아니지만 이해를 돕기 위해서 종류를 구분하여 설명하겠습니다. 아래 영문으로 기재된 초기화 기법의 이름은 keras initializer[2]에서 가져왔습니다.
1. 상수 기반 초기화 (Zeros. Ones, Constant)
정해진 숫자를 기반으로 웨이트 값을 초기화 합니다. 0으로 초기화하면 Zeros, 1로 초기화 하면 Ones, 사용자가 지정한 상수로 초기화하면 Constant 기법입니다.
사용처: 실제로는 잘 사용되어 지지 않습니다. 유용한 사용처를 아시는 분이 계시다면 댓글로 남겨주시면 감사하겠습니다.
한계점: 모든 웨이트들이 동일한 값으로 초기화 되어 학습 초기에 모든 웨이트 값들이 동일한 출력을 내게 됩니다.
2. 선형 대수 기반 초기화 (Orthogonal, Identity)
선형대수에 등장하는 개념을 기반으로 웨이트 값을 초기화 합니다. Orthogonal이란 선형 대수에서 직교라는 뜻입니다. Orhogonal 웨이트 초기화란 직교 행렬이 되게끔 matrix 형태의 웨이트 값을 초기화 하겠다는 의미입니다. 직교 행렬이란 자기 자신과 자신의 전치 행렬의 곱이 항등행렬이 되는 행렬을 말합니다. 직교 행렬에 대한 자세한 개념은 생략하며 궁금하신 분들은 다음 자료를 참고해주세요.[3] Identity 기법은 항등행렬로 초기화 하겠다는 의미이며 우리가 흔히 아는 [[1, 0], [0. 1]] 이렇게 대각선이 1이고 나머지가 0인 행렬을 말합니다.
사용처: 실제로는 잘 사용되어 지지 않습니다. 유용한 사용처를 아시는 분이 계시다면 댓글로 남겨주시면 감사하겠습니다.
한계점: 주어진 조건에만 맞도록 랜덤하게 초기값을 설정하여 특정 값이 지나치게 크거나 작아질 수 있습니다. 이는 레이어들의 출력 값이 들쑥날쑥하게 만들어 학습을 어렵게 만듭니다.
3. 확률 분포 기반 초기화 (RandomUniform, RandomNormal, TruncatedNormal)
특정한 확률 분포에 기반하여 랜덤한 값을 추출하여 웨이트를 초기화 합니다. (확률 분포에 대한 자세한 내용은 제 이전 포스팅을 참고해주시면 감사하겠습니다.) 이 때 UniformDistribution과 NormalDistribution이 사용됩니다. 각각의 확률 분포의 그래프는 아래와 같습니다.

먼저 UniformDistribution은 최소값과 최대값 사이의 값들이 동일한 확률로 추출되는 분포입니다. keras에서는 기본적으로 -0.05에서 0.05 사이의 값을 동일한 확률로 추출하도록 설정되어 있습니다. RandomUniform 함수를 통해 사용이 가능합니다.
다음으로 우리에게 친숙한 종모양의 정규분포입니다. 평균에 가까운 값일수록 더 높은 확률로 추출이 됩니다. keras에서는 기본적으로 평균이 0, 표준편차가 0.05인 정규 분포에서 값을 추출하도록 설정되어 있습니다. RandomNormal 함수를 통해 사용이 가능합니다.

마지막으로 TruncatedNormal입니다. 이는 정규 분포에서 초기화 값을 추출하되, 평균으로부터 표준 편차의 두 배가 넘는 값들은 버리고 다시 추출하는 방식을 의미합니다. 위 도표를 참고해보면 평균에서 표준 편차의 두배의 값의 범위 안에는 약 95%의 데이터가 분포하는 것을 확인할 수 있습니다. 그 밖의 값을 버리겠다는 것은 특이값을 제거하겠다는 의미입니다. 이 다음 등장하는 분산 조정 기법에서 자주 사용됩니다.
사용처: 초기 신경망들이 이러한 방식을 사용했다고 합니다. 작은 신경망을 학습시키는 상황에서는 충분히 잘 작동한다고 합니다.
한계점: 레이어가 깊어질 수록 전체 신경망에 걸쳐 non-homogeneous distributions of activations를 생성한다고 합니다. (원문이 더 직관적이어서 그대로 옮겼습니다.) activation이 0에 수렴하여 vanishing gradient 문제의 원인이 됩니다.[3]
4. 분산 조정 기반 초기화(Glorot, Lecun, He)
드디어 실제 딥 러닝 모델들에서 가장 많이 사랑받는 기법에 도착했습니다. 분산 조정 기법이란 확률 분포를 기반으로 추출한 값으로 웨이트를 초기화 하되, 이 확률 분포의 분산을 웨이트 별로 동적으로 조절해주자는 것입니다. 그리고 분산을 조정할 때에는 해당 웨이트에 input으로 들어오는 텐서의 차원(fan in)과 결과 값으로 출력하는 텐서의 차원(fan out)이 사용됩니다.
사용처: 실제로 현재 신경망을 초기화 시키는 방법으로 사용됩니다.
한계점: 각각의 초기화 방법 역시 완벽한 것은 아니며, 더 나은 초기화 방법을 찾기 위한 연구들이 지금도 진행되고 있습니다. 관심있으신 분들은 관련된 서베이 논문들을 찾아보시면 좋을 것 같습니다.
이를 이해하기 위해서 먼저 fan in과 fan out의 개념을 살펴보아야만 합니다.
fan in fan out
fan in이란 해당 레이어에 들어오는 input tensor의 차원 크기입니다. fan out은 레이어가 출력하는 output tensor의 크기입니다. Dense Layer (Fully Connected Layer)의 경우에는 이것이 직관적으로 와닿습니다. 1000 x 200 크기의 FC 레이어의 fan in은 1000, fan out은 200이 됩니다. 하지만 CNN과 RNN의 경우에는 좀 더 복잡해집니다. 가장 보편적으로 사용되는 Conv2D 레이어에서 어떻게 fan in과 fan out을 계산하는 지를 보며 익혀보겠습니다. 구체적인 계산 방법은 tensorflow 소스 코드[6]를 참고하였습니다.


위 예시는 32x32x3 크기의 이미지를 입력으로 받아 5x5 크기의 커널을 6체널 적용하여 28x28x6 크기의 activation map을 생성하는 간단한 컨볼루션 레이어의 연산을 시각화하였습니다. 이 레이어의 fan in과 fan out을 계산하려면 먼저 커널의 모양을 알아야 합니다. 커널 모양의 수식은 아래와 같습니다.

이 커널 모양을 기반으로 receptive field 값을 계산합니다. receptive field란 전체 인풋에서 해당 커널이 얼만큼 인식하는 지를 나타내며 수식은 아래와 같습니다. Π 기호는 피, 혹은 파이라고 읽으며 해당 범위 내의 모든 값의 총 곱을 나타냅니다. 시그마의 곱셈 버전으로 생각하면 됩니다. k는 kernel shape의 차원 수로 여기서는 4입니다.

이제 receptive field 값과 kernel shape를 이용하여 fan in과 fan out을 계산합니다. 위 사례에 대입해보면 각각 75와 150이 나오는 것을 확인 할 수 있습니다.

Conv2D의 사례를 통해서 알아보았지만 이러한 계산 방식은 다른 신경망 구조들에도 동일하게 적용할 수 있습니다. Conv3D, Conv4D나 LSTM과 같은 블럭들도 kernel shape와 receptive field를 계산하면 이를 이용하여 fan in과 fan out을 구할 수 있습니다.
Lecun Initialization
· keras 구현체
- lecun_uniform
- lecun_normal
초기 CNN인 lenet으로 유명한 Yann Lecun 교수님의 1998년 페이퍼에서 제안된 기법입니다. 기본적으로 uniform distribution 혹은 normal distribution에서 추출한 랜덤 값으로 웨이트를 초기화 시키되, 이 확률 분포를 fan in값으로 조절하자는 아이디어입니다. 수식으로 표현하면 아래와 같습니다.
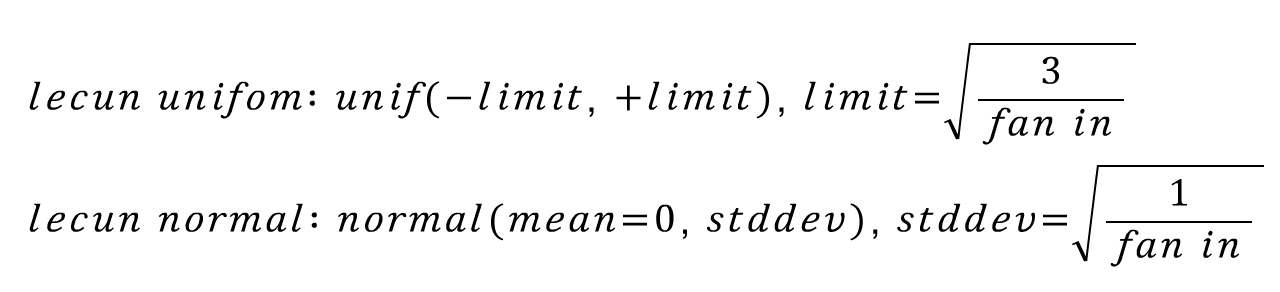
핵심 아이디어는 신경망에 들어오는 input의 크기가 커질 수록 초기화 값의 분산을 작게 만들자는 것입니다. 그 결과로 0에 가까운 더 작은 값들이 추출되게 됩니다. 또한 truncated 기법을 적용하여 범위를 벗어나는 특이값들은 배제합니다.
Xavier Glorot Initialization
· keras 구현체
- glorot_uniform
- glorot_normal
다음으로 현재에도 가장 많이 사용되는 초기화 기법인 Xavier Glorot Initialization입니다. Xavider Initialization, Glorot Initialization이라고도 불립니다. Xavier Glorot과 Yosua Bengio 교수님이 2010년에 발표한 페이퍼[5]에서 제안되었습니다. 수식으로 살펴보면 아래와 같습니다.
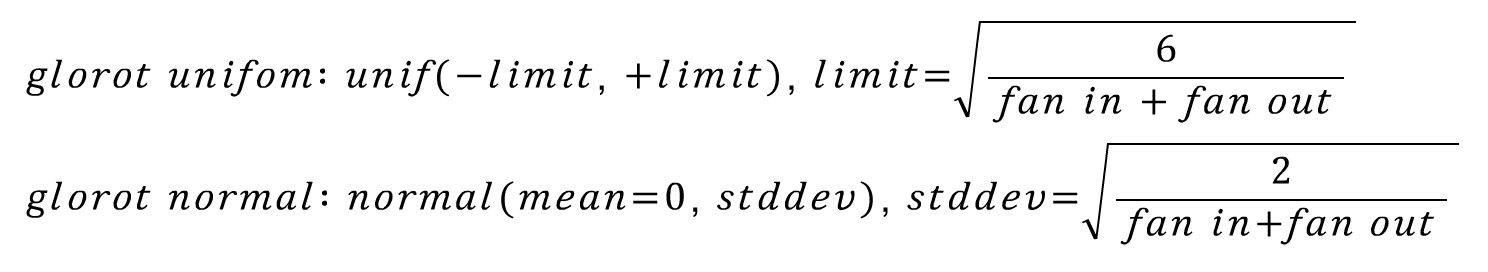
핵심 아이디어는 fan in과 fan out을 모두 고려하여 확률 분포를 조정해준다는 것입니다. lecun initialization 기법에서 2를 곱해준 뒤, fan in과 fan out의을 합한 크기로 나누어 준 값으로 확률 분포를 조정합니다.
tanh를 활성화 함수로 사용하는 신경망에서 많이 사용됩니다. 또한 glorot_uniform은 keras에서 기본 초기화 방법으로 사용됩니다. 하지만 ReLU를 활성화 함수로 사용할 때에는 잘 작동하지 않는 모습을 보인다고 하며, 후에 He Initialization이 제안되는 배경이 됩니다.
He Initailization
· keras 구현체
- he_uniform
- he_normal
Glorot 기법의 한계를 극복하기 위해 Kaming He가 2010년 발표한 페이퍼[7]에서 제안한 기법입니다. 또한 ResNet을 학습시킬 때 이 기법을 사용하여 실제로 깊은 CNN 신경망을 학습시킬 때 잘 작동함을 보여주었습니다. 수식으로 표현하면 아래와 같습니다.

수식을 살펴보면 glorot 기법에서 다시 fan out을 제거한 모습을 보입니다. ReLU 함수가 아무래도 0 이하의 activation 값들은 모두 제거하므로 fan in을 더 중요하게 고려한 듯 합니다. 그 결과로 lecun initializaion에서 2를 곱해준 형태를 취해주게 됩니다. ReLU가 activation으로 사용되는 신경망을 초기화 할 때 많이 사용됩니다.
마치며
지금까지 웨이트를 초기화 하는 다양한 기법들에 대해서 알아보았습니다. 작은 차이들이 학습 결과에 큰 영향을 준다는 것이 참 신기하네요. 사실 각각의 초기화 기법의 대략적인 수식과 특징에 대해서만 알아보는 수준에서 그쳐서 아쉬움이 남습니다. 그 이상의 학문적인 내용들은 너무 어렵기도 하고 내용이 방대하여 깊이 있게 다루기에 무리가 있었습니다.
추가적으로 더 궁금하신 분들은 레퍼런스에 달려있는 페이퍼들을 직접 읽어보시거나 영문으로 된 블로그 포스팅들을 읽어보시면 좋을 것 같습니다.
감사합니다.
Reference
[1] Hyper parameters in Action, https://towardsdatascience.com/hyper-parameters-in-action-part-ii-weight-initializers-35aee1a28404
[2] initializer, https://keras.io/initializers/, keras
[3] cs231n, https://www.youtube.com/watch?v=GUtlrDbHhJM&list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm, Andreji Karpathy
[4] Efficient BackProp, Lecun et al, 1998
[5] Understanding the difficulty of training deep feedforward neural networks, Xavier et al, 2010
[6] keras source code, https://github.com/keras-team/keras/blob/7a39b6c62d43c25472b2c2476bd2a8983ae4f682/keras/initializers.py#L462, github
[7] delving deep into rectifier, he et al, 2010
'갈아먹는 머신러닝 시리즈 > 딥러닝 기초' 카테고리의 다른 글
| 🧠 갈아먹는 딥러닝 기초 (0) | 2023.10.26 |
|---|---|
| 갈아먹는 딥러닝 기초 [1] Activation Function(활성화 함수) 종류 (3) | 2020.04.24 |
| 갈아먹는 자격증 [1] Tensorflow Certificate 취득 안내 및 후기 (26) | 2020.04.08 |
