지난 글
들어가며
우리는 지금까지 데이터를 특정한 확률 분포를 가진 확률 변수로 모형화 하였습니다. 그리고 모집단의 표본에서 얻은 통계량을 통해 모집단의 통계적 특성을 추측해보았습니다. 이러한 과정을 논리적으로 전개하기 위해서 필요한 것이 가설과 검정입니다.
가설(hypothesis)란 확률 분포에 대한 어떠한 주장이며 이를 증명하는 행위를 검정(testing)이라 합니다. 특히 확률 분포의 모수 값에 대한 가설을 검정하는 것을 모수 검정(parameter testing)이라 부릅니다.
귀무 가설과 대립가설
귀무 가설(null hypothesis, 영 가설)은 처음부터 버릴 것을 예상하는 가설입니다. 기본적으로 참으로 추정되며 이를 거부하기 위해서는 증거가 반드시 필요합니다. 예를들어 형사가 용의자를 잡았을 경우에도 무죄 추정의 원칙에 따라서 '이 용의자는 무죄일 것이다' 라는 가설을 먼저 세우게 됩니다.[1] 귀무 가설을 세울 때에는 특별한 증거가 없다면 참으로 여겨지는 가설을 귀무 가설로 세우게 됩니다.
대립 가설(alternative hypothesis)는 귀무 가설과 대립되는 가설을 말합니다. 위 예시를 대입해보면 '이 용의자가 범인일 것이다!'가 됩니다. 일반적으로 연구자는 연구를 통해 귀무 가설을 검증하게 되고, 이를 통해서 대립 가설이 입증되기를 기대합니다. 즉, 용의자가 무죄일 것이다를 전제로 하고 이를 깨기 위해 열심히 증거를 찾게 되는 것입니다.
귀무 가설과 대립 가설을 기호로 표현하면 아래와 같습니다.

가설 설정의 규칙
통계적 가설을 세울 때에는 다음의 규칙을 따라야 합니다.[3]
1. 귀무 가설은 모수를 특정한 값으로 표현한다. H0:θ=θ0
2. 대립 가설은 귀무 가설에서 지적한 모수의 값이 아닌 어떤 영역으로 나타내는데, 양쪽을 다 고려하는 양측 검정과 한쪽만 고려하는 단측 검정이 있다.

검정과 검정 오류
가설은 맞다, 틀리다로 이분법적으로 답을 내릴 수 있는 문제가 아닌 정도의 문제입니다. 귀무 가설이 틀릴 확률이 얼마이므로 이를 기각한다 / 기각하지 못한다와 같은 형태로 표현할 수 있습니다. 이렇듯 우리는 가설이 틀릴 가능성에 초점을 맞추고 검정을 진행하게 되는데 이 때, 가설이 틀릴 가능성에 대해서 제 1종 오류와 제 2종 오류로 구분합니다.
제 1종 오류(type 1 error)란 귀무 가설이 맞는데도 이를 잘못 기각하여 발생하는 오류입니다. 용의자가 무죄가 맞지만 잘못하여 유죄 판결을 내리는 것과 같습니다. 제 2종 오류(type 2 error)란 대립 가설이 사실임에도 불구하고 귀무가설을 기각하지 못하는 오류를 말합니다. 용의자가 범인이 맞지만 무죄가 아니라는 것을 입증해내지 못하는 것을 말합니다.
제 1종 오류가 발생할 확률을 α라고 표기하고 검정의 유의수준(significance level)이라 합니다. 반대로 제 2종 오류가 발생할 확률을 β라고 표기합니다. 대립 가설이 사실일 때 귀무 가설을 기각할 확률 (1- β)를 검정력이라고 표현합니다. 표로 나타내면 아래와 같습니다.

가설의 검정에서는 이 두 가지 오류인 α, β를 최소로 하는 임계값 c를 결정하고 기각역을 설정하는 것이 중요합니다. 하지만 임계값을 높게 설정하면 β가 커지고, 그렇다고 낮게 설정하면 α가 커지는 모순 관계에 놓여 있습니다. 그렇기 때문에 α를 고정시키고, 이를 만족 시키는 기각역 중에 β를 최소화하는 기각역을 선택하게 되고, 그렇기 때문에 1- β를 검정력이라고 부르는 것입니다. 고정시키는 α 값은 학문 분야에 따라서 다른데 사회과학 분야는 보통 0.05, 자연 과학 분야는 0.01이라는 가이드라인을 제시한다고 합니다.

이제 귀무 가설을 기각하여 일만 남았으며, 우리는 두 가지 방법을 사용할 수 있습니다.
· p-value 사용하기
· 기각역(rejection area) 사용하기
개념만 말로 설명하기엔 다소 까다로울 수 있으므로 예제를 하나 풀어보면서 진행하도록 하겠습니다. [3]
Q: 한 쪽은 한국 청소년들의 TV 시청 시간이 평균 3시간이라고 주장합니다. 다른 측은 3시간보다 작을 것이라 주장합니다. 어느 편이 맞는지 알아보기 위해 임의로 추출한 100명을 조사한 결과 평균 2.75 시간이었습니다. TV 시청 시간은 정규 분포를 하며 분산은 과거 조사에서 1로 알려져 있습니다.

p-value(유의 확률)를 사용한 검정
먼저 p-value를 사용하여 귀무 가설을 기각해보도록 하겠습니다. p-value란 귀무 가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 관측될 확률입니다. 귀무 가설이 맞다고 치면 평균 TV 시청 시간은 3시간입니다. 이를 정규화하여 표준 정규 분포 상으로 그려보면 아래와 같습니다.

파란색 직선은 검정 통계량, 즉 실제 표본의 관측을 통해서 얻은 표본 평균의 z-score입니다. 실제로 관측해본 결과 TV 시청 시간의 평균의 Z-score는 -2.5라는 의미입니다. 파란색 직선 왼쪽의 영역은 대립가설의 방향으로 치우쳐서 발생하는 사건의 확률이며 아래 그래프에서 파란색 영역에 해당합니다. 이 확률 값을 p-value라고 부릅니다.
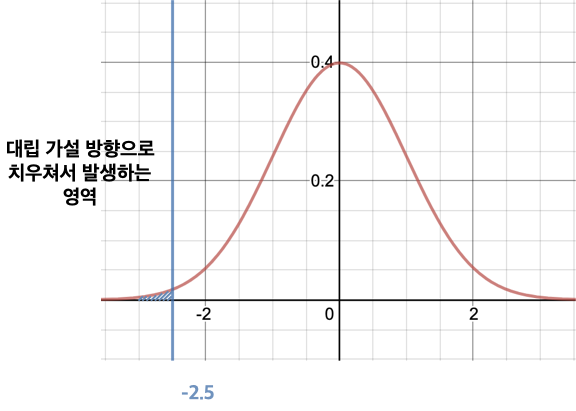
이를 표준 정규 분포표를 통해서 계산해보면 p-value는 0.0062가 됩니다. 앞서 우리는 귀무가설이 틀릴 수 있는 확률 α를 0.05로 고정해놓았습니다. 자 그렇다면 실제 관측을 진행할 때 파란색 직선 좌측에 해당하는 값이 등장했다고 생각해보겠습니다. 귀무 가설이 옳았더라면 이러한 값이 나올 확률은 0.0062입니다. 하지만 이보다는 귀무 가설이 옳지 않았을 확률인 0.05가 더 높습니다. 이는 곧 귀무 가설이 옳지 않았다라는 주장이 더 설득력이 있으므로 귀무 가설이 기각되는 것입니다.

위의 예시는 단측 검정이었기 때문에 정규 분포의 왼쪽 꼬리 부분만 고려하였습니다. 만일 양측 검정이라면 양쪽 양향으로 극단적인 값이 등장할 확률을 계산해야하며, 아래 그래프 상에서 빨간색 면적에 해당합니다.

p-value를 쉬운 말로 간단히 설명하고 넘어가겠습니다. 유의 확률이라는 말에서 알 수 있듯이 이는 가설이 얼마나 그럴듯 한지를 나타내주는 값이며 0부터 1 사이의 값을 가집니다. p 값이 0에 가까울수록 귀무가설의 설득력은 점점 약해지고 이를 기각하고 우리가 입증하고 싶은 대립 가설의 설득력은 점점 강해지게 됩니다.
기각역을 사용한 검정
앞서 p-value를 사용하여 귀무 가설을 기각했을 때 우리는 귀무 가설이 틀릴 확률 α 값을 사용하였습니다. 그리고 p-value가 α보다 작다면 귀무 가설을 기각하였습니다. 그렇다면 반드시 p-value를 구하지 않고서도 α만으로 귀무 가설이 기각될 수 있는 영역을 찾아낼 수 있지않을까요?

위 그래프에서 파란색 면적에 해당하는 부분이 귀무 가설이 틀릴 확률 α에 해당합니다. 만일 검정 통계량이 저 파란색 영역에 속하게 된다면 p-value가 α값보다 작아지므로 귀무가설이 기각되게 됩니다. 즉, 파란색 영역은 귀무 가설이 기각되는 기각역(rejection region)에 해당합니다. 예제에서 검정 통계량의 z-score는 -2.5로 기각 역에 속하게 되므로 귀무 가설을 기각할 수 있습니다.
마치며
지금까지 통계학에서 가설을 어떻게 세우고 검정을 어떻게 진행하는지 알아보았습니다. 그리고 p-value와 기각역을 사용하여 귀무 가설을 기각하는 방법을 알아보았습니다. 사실 p-value에 대한 설명이 교과서나 외부 자료에서도 지나치게 복잡하게 설명되어 있는 감이 있어서 최대한 직관적으로 이해할 수 있게끔 설명해보고자 노력해 보았는데 어떨지 모르겠네요...ㅎㅎ설명이 부족하다고 느껴지시면 댓글로 알려주세요!
감사합니다.
Reference
[1] 귀무 가설, https://ko.wikipedia.org/wiki/%EA%B7%80%EB%AC%B4_%EA%B0%80%EC%84%A4, wikipedia
[2] 검정과 유의확률, https://datascienceschool.net/view-notebook/37a330dfc8de45e9ba475cbbd201ab53/, 데이터 사이언스 스쿨
[3] 통계학 입문, 강상욱 외 8인
'갈아먹는 머신러닝 시리즈 > 통계학 기초' 카테고리의 다른 글
| 📊 갈아먹는 통계학 (0) | 2023.10.26 |
|---|---|
| 갈아먹는 통계 기초[3] 표본 추출 (0) | 2020.04.19 |
| 갈아먹는 통계 기초[2] 공분산과 피어슨 상관 계수 (0) | 2020.04.19 |
| 갈아먹는 통계 기초 [1] 확률 분포 정리 (3) | 2020.04.18 |
